3.4. Hyperparameter Optimization (Model Tune)¶
Hyperparameter tuning is a crucial step in the process of training machine learning models. Examples of hyperparameters include learning rate, batch size, the number of hidden layers in a neural network, and the number of trees in a random forest.
The goal of hyperparameter tuning is to find the optimal set of hyperparameters that maximizes the performance of a model on a given task. The process involves experimenting with different hyperparameter values and assessing their impact on the model’s performance. The performance is typically evaluated using a validation set or through cross-validation.
3.4.1. Methodology¶
In PiML, we integrate two common techniques used in hyperparameter tuning:
Grid Search: This is a brute-force approach where a predefined set of hyperparameter values is specified, and the model is trained and evaluated for all possible combinations. While comprehensive, it can be computationally expensive. The grid search in PiML is implemented based on scikit-learn’s GridSearchCV.
Random Search: In contrast to grid search, random search involves randomly selecting a combination of hyperparameter values from a predefined range. This method is more efficient than grid search and often yields similar or better results. The random search in PiML is implemented based on scikit-learn’s RandomizedSearchCV.
3.4.2. Usage¶
As an experiment is initialized with data and models, we can use the function exp.model_tune to tune the models. The function incorporates several key parameters:
method: The method parameter dictates the search strategy employed, offering options between ‘grid’ and ‘randomized’ search methods.parameters: This parameter allows you to define the search space through a dictionary. Keys in the dictionary represent parameter names (as strings), and corresponding values are lists of values to be explored. It is usually set as a list of candidate values, e.g., {‘kernel’: [‘linear’, ‘rbf’], ‘alpha’: np.linspace(0, 1, 20)}. For random search, you can also specify distributions using scipy.stats distributions, e.g., {‘alpha’: scipy.stats.uniform(0, 1)}.metric: Determines the evaluation metrics for model tuning. It can be a single metric or a list of metrics. For regression tasks, options include “MSE,” “MAE,” and “R2.” For classification tasks, metrics including “ACC,” “AUC,” “F1,” “LogLoss,” and “Brier” are available. The default is “MSE” for regression and “ACC” for classification.n_runs: Relevant only when the search method is ‘randomized,’ specifying the number of runs or iterations during the search process.cv: Defines the number of folds for cross-validation. By default, set as None, indicating the use of hold-out validation. If cross-validation is desired, set it as an integer.test_ratio: If cv is None, this parameter determines the proportion of the training set (default is 20%) allocated for validation in the absence of cross-validation.
3.4.2.1. Get model tunning result¶
Assume we have already fitted an XGB2 model via PiML. Next, we can use the exp.model_tune function to optimize its hyperparameters, as shown below.
parameters = {'n_estimators': [100, 300, 500],
'eta': [0.1, 0.3, 0.5],
'reg_lambda': [0.0, 0.5, 1.0],
'reg_alpha': [0.0, 0.5, 1.0]}
result = exp.model_tune("XGB2", method="grid", parameters=parameters, metric=['MSE', 'MAE'], test_ratio=0.2)
In this example, we begin by defining the hyperparameter search space. Specifically, we target the tuning of four hyperparameters in XGBoost (‘n_estimators’, ‘eta’, ‘reg_lambda’, and ‘reg_alpha’). Each hyperparameter is assigned three candidate values. Subsequently, the model tuning API in PiML is invoked, employing grid search for the optimization process.
For the assessment of model performance, we utilize a hold-out validation set, constituting 20% of the original training set. The evaluation metrics employed are ‘MSE’ (Mean Squared Error) and ‘MAE’ (Mean Absolute Error). Upon executing the code, we can proceed with a detailed analysis of the obtained results.
result.data
result.plot(param='n_estimators', figsize=(6, 4.5))
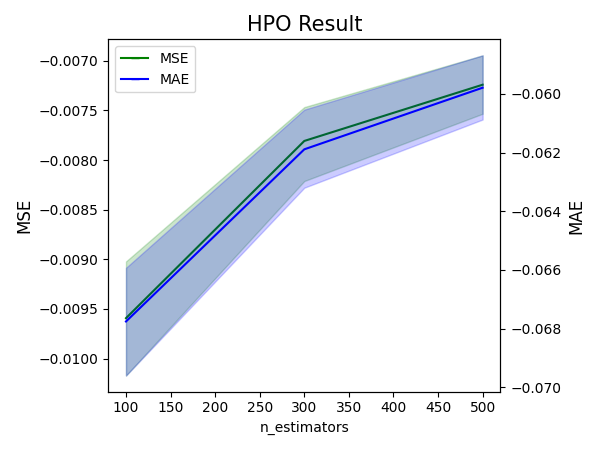
In the context of this plot, metrics that are considered better when smaller are all negated. Consequently, the expectation is that all metrics displayed in the plot should be larger for better performance.
In practice, achieving optimal predictive performance is not the sole objective of modeling. There is often a preference for simpler models, even if there is a trade-off in predictive accuracy. Model developers can manually identify the most suitable hyperparameter configuration by examining the tables and plots presented above.
The result object incorporates a built-in function known as “get_params_rank,” enabling the retrieval of parameters based on the specified rank ID from the results. After determining the best parameters, a refined model can be trained and subsequently registered within the PIML experiment.
params = result.get_params_ranks(rank=1)
exp.model_train(XGB2Regressor(**params), name="XGB2-HPO-GridSearch")
The codes above first retrieve the top-1 hyperparameter, i.e., {‘eta’: 0.5, ‘n_estimators’: 500, ‘reg_alpha’: 0.5, ‘reg_lambda’: 0.0}, and refit the model using the exp.model_train API.
3.4.3. Examples¶
There are two HPO example codes in the following link.
