4.3. Hstats (Friedman’s H-statistic)

H-statistic measures the interaction strength of two features [Friedman2008].

4.3.1. Algorithm Details

Consider a set of features, represented by \(X\), and a fitted model, represented by \(\hat{f}\). The H-statistic is defined based on partial dependence, as follows:

\[\begin{align} H_{j k}^2=\frac{\sum_{i=1}^n\left[P D_{j k}\left(x_j^{(i)}, x_k^{(i)}\right)-P D_j\left(x_j^{(i)}\right)-P D_k\left(x_k^{(i)}\right)\right]^2}{\sum_{i=1}^n P D_{j k}^2\left(x_j^{(i)}, x_k^{(i)}\right)}, \tag{1} \end{align}\]

where feature \(j\) and \(k\) are two features in \(X\), \(x_j^{(i)}\) and \(x_k^{(i)}\) are the values of features \(j\) and \(k\) for the \(i\)-th sample, respectively, and \(PD_{jk}(x_j^{(i)}, x_k^{(i)})\) is the partial dependence of \(\hat{f}\) on features \(j\) and \(k\) at \((x_j^{(i)}, x_k^{(i)})\). The H-statistic is a measure of the interaction strength between features \(j\) and \(k\). The larger the H-statistic, the stronger the interaction between features \(j\) and \(k\). The H-statistic is symmetric, i.e., \(H_{jk}=H_{kj}\).

4.3.2. Usage

H-statistic can be calculated using PiML’s model_explain function. The keyword for PDP is “hstats”, i.e., we should set show = “hstats”. Additionally, the following arguments are relevant to this analysis:

  • use_test: If True, the test data will be used to generate the explanations. Otherwise, the training data will be used. The default value is False.

  • sample_size: To speed up the computation, we subsample a subset of the data to calculate PDP. The default value is 2000. To use the full data, you can set sample_size to be larger than the number of samples in the data.

  • grid_size: The number of grid points in PDP. The default value is 10.

  • response_method: For binary classification tasks, the PDP is computed by default using the predicted probability instead of log odds; If the model does not have “predict_proba” or we set response_method to “decision_function”, then the log odds would be used as the response.

The following code shows how to calculate the H-statistic of a fitted XGB2 model.

exp.model_explain(model="XGB2", show="hstats", sample_size=2000, grid_size=5,
                  figsize=(5, 4))
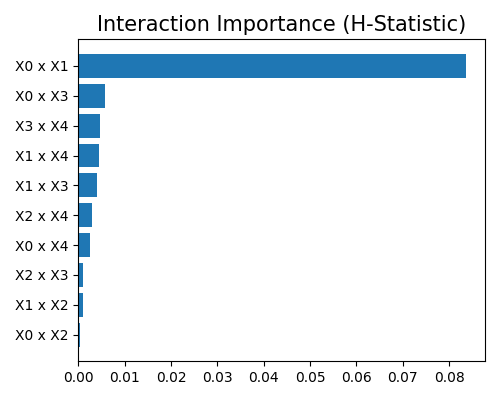
../../_images/sphx_glr_plot_1_pdp_hstats_001.png

The plot above lists the top-10 important interactions. To get the H-statistic of the full list of interactions, we can set return_data=True, and the H-statistic of all interactions will be returned as a dataframe, as shown below.

result = exp.model_explain(model="XGB2", show="hstats", sample_size=2000, grid_size=5,
                           return_data=True, figsize=(5, 4))
result.data
Feature 1 Feature 2 Importance
0 X0 X1 8.354665e-02
1 X0 X3 5.772886e-03
2 X3 X4 4.769194e-03
3 X1 X4 4.488876e-03
4 X1 X3 3.939141e-03
5 X2 X4 2.891201e-03
6 X0 X4 2.615382e-03
7 X2 X3 1.110027e-03
8 X1 X2 9.062784e-04
9 X0 X2 4.224594e-04
10 X4 X7 4.187721e-04
11 X6 X9 2.826716e-04
12 X1 X6 2.798646e-04
13 X1 X9 2.139691e-04
14 X0 X9 1.499676e-04
15 X2 X9 1.367038e-04
16 X3 X9 1.256837e-04
17 X0 X6 1.022405e-04
18 X3 X6 1.017541e-04
19 X2 X5 3.553405e-06
20 X4 X6 2.510080e-06
21 X1 X5 2.003126e-06
22 X2 X6 2.001398e-06
23 X0 X8 9.355216e-07
24 X1 X8 8.842721e-07
25 X7 X9 3.703580e-07
26 X2 X8 3.405027e-07
27 X4 X8 2.302398e-07
28 X0 X7 2.020537e-07
29 X5 X8 6.266068e-08
30 X5 X7 4.271688e-08
31 X0 X5 3.382035e-09
32 X7 X8 2.910548e-09
33 X5 X6 1.166214e-09
34 X6 X7 5.757503e-10
35 X6 X8 4.158681e-10
36 X5 X9 2.689033e-10
37 X8 X9 2.289872e-10
38 X4 X5 1.034555e-12
39 X4 X9 5.418748e-13
40 X2 X7 1.989873e-13
41 X3 X8 1.310739e-13
42 X3 X5 1.203739e-13
43 X1 X7 7.804507e-14
44 X3 X7 5.885018e-14

4.3.3. Examples