5.9. ReLU Neural Network

Deep neural networks (DNNs) that use the rectified linear unit (ReLU) activation functions have achieved remarkable success. Due to its simple functional form, ReLU offers many appealing properties, such as a fast convergence rate, excellent predictive performance, and intrinsic interpretability. In this section, we will give a brief overview of the ReLU-DNN model and how it is used in PiML.

5.9.1. Model Formulation

Consider a feedforward ReLU network with inputs \(\textbf{x} \in \mathbb{R}^{d}\), \(L\) hidden layers, and one output neuron. Assume the \(l\)-th hidden layer has \(n_{l}\) neurons. In particular, we mark the input layer as a special hidden layer with index 0 (\(n_{0}=d\)). The weight matrix and bias vector of the \(l\)-th hidden layer to the \((l+1)\)-th hidden layer are denoted by \(\textbf{W}^{(l)}\) of size \(n_{l+1}\times n_{l}\), and \(\textbf{b}^{l}\) of size \(n_{l+1}\), respectively. Let \(\textbf{z}^{(l)}\) denotes the input of the \(l\)-th hidden layer. Then, the network can be recursively expressed by

\[\begin{align} \textbf{z}^{(l + 1)}=\textbf{W}^{(l)}\chi^{(l)}+\textbf{b}^{(l)}, \mbox{for } l=0,\ldots,L-1, \tag{1} \end{align}\]

where \(\chi^{(l)}\) is the output of the \(l\)-th hidden layer after the ReLU transformation

\[\begin{align} \chi^{(l)} = max\{0,z^{(l)}\}, \mbox{for } l=1,\ldots, L. \tag{2} \end{align}\]

Finally, the output layer (i.e., the layer \(L + 1\)) is given by

\[\begin{align} \mathbb{E}[y]=\sigma(\eta(\textbf{x}))=\sigma(\textbf{W}^{(L)}\chi^{(L)}+\textbf{b}^{(L)}), \tag{3} \end{align}\]

where \(\textbf{b}^{(L)}\) is the bias of the output layer, and \(\sigma\) is the activation function, which can be identity (regression) or sigmoid (binary classification).

5.9.2. Local Linear Models

Despite the complex model form, the black box of deep ReLU networks can be unwrapped through local linear representations [Sudjianto2020]. First of all, let’s define the activation pattern.

Activation Pattern: Let the binary vector \(C=[C^{(1)}; \ldots; C^{(L)}]\) indicate the on/off state of each hidden neuron in the network. Specifically, the component \(C^{(l)}\) is called a layered pattern for \(l=1,\ldots,L\). The activation pattern \(C\) is said to be trivial if there is at least one \(C^{(l)} \equiv 0\) for some \(l\).

The length of the activation pattern is \(\sum_{i=1}^L n_l\), i.e., the total number of hidden neurons in the network. Each sample \(\textbf{x}\) corresponds to a particular activation pattern of the form

\[\begin{equation} C(\textbf{x}) = [C^{(1)}(\textbf{x}); \ldots; C^{(L)}(\textbf{x})]. \end{equation}\]

Data points that exhibit the same activation pattern can be grouped, and their input-output relationship can be simplified using a linear model, known as the local linear model (LLM). By disentangling the network, an equivalent set of LLMs can be obtained.

\[\begin{align} \eta(\textbf{x}) = \tilde{\textbf{w}}^{C(\textbf{x})}\textbf{x} + \tilde{b}^{C(\textbf{x})}, \tag{4} \end{align}\]

where \(\tilde{\textbf{w}}^{C(\textbf{x})}\) and \(\tilde{b}^{C(\textbf{x})}\) are the coefficients and intercept of the linear model, which can be obtained by some matrix operations of hidden layers weights and biases, considering the corresponding hidden neuron on/off states. The LLM extraction algorithm has been implemented in the Python package Aletheia, and most of its functionalities have been directly integrated into the PiML package.

5.9.3. Model Training

In this section, we demonstrate how to train a ReLU-DNN model using PiML. Assuming the data is already prepared, then the ReLU-DNN model can be imported and fitted using PiML’s built-in workflow, as shown below.

from piml.models import ReluDNNClassifier
exp.model_train(model=ReluDNNClassifier(hidden_layer_sizes=(40, 40), l1_reg=0.0002, learning_rate=0.001),
                name="ReLUDNN")

Below we briefly introduce some of the most important hyperparameters in the ReLU-DNN model.

• hidden_layer_sizes: a tuple used to specify the hidden layer structure, by default (40, 40), which means a ReLU-DNN with two hidden layers, each with 40 nodes. The hidden layer size is important for the model’s performance and interpretability. A small-sized ReLU-DNN may be of limited expressive power, and hence, poor model performance. However, if the network size is too large, the model can be extremely complicated and therefore hard to interpret. In practice, it is recommended to start with a relatively larger network size and then apply the L1 penalty to reduce its complexity.

• l1_reg: the regularization strength that penalizes the weights, by default 1e-5. In each gradient descent iteration, it shrinks the network weights toward zero, while the bias terms keep unpenalized. Applying the L1 penalty to the network weights may avoid overfitting and enhance model interpretability. In practice, by increasing l1_reg, the resulting model tends to have a smaller number of LLMs.

• learning_rate: a float that controls the step size of gradient descent, by default 0.001. The choice of learning rate is critical for model performance. A small learning_rate may result in an unnecessarily long training time, whereas a large one may make the training process unstable.

For the full list of hyperparameters, please see the API of ReluDNNRegressor and ReluDNNClassifier.

5.9.4. Global Interpretation

Assume a ReLU-DNN model is fitted. Then, it can be inherently interpreted.

5.9.4.1. LLM Summary Table

In exp.model_interpret, we can set the parameter show to “llm_summary” to get the summary statistics for each LLM.

exp.model_interpret(model="ReLUDNN", show="llm_summary")

In the summary table above, each row represents an LLM with the following statistics.

• count: The number of training samples

• Response Mean: The average of the response values

• Local AUC: The local performance of this LLM in its local region

• Global AUC: The global performance when using this LLM for all training samples

Such information can help model developers to have a better understanding of the fitted ReLU-DNN model. For example, the first row indicates that the largest LLM has 5153 training samples, with an average response value of 0.105570, a local AUC of 0.584421, and a global AUC of 0.735054. From the results, we find that this LLM’s global performance is even better than its local performance, and a simpler model like GLM may be good enough.

5.9.4.2. Parallel Coordinate Plot

The parallel coordinate plot can be used by setting show to “llm_pc”.

exp.model_interpret(model="ReLUDNN", show="llm_pc", figsize=(5, 4))

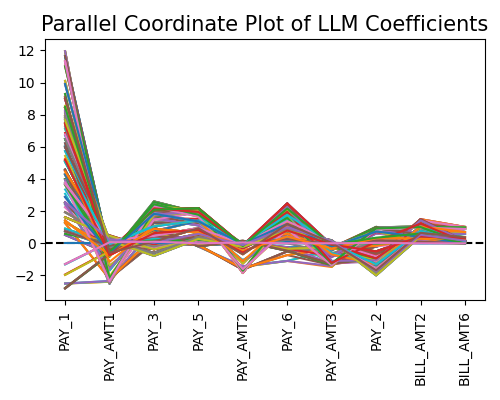
This plot is used for visualizing coefficients of different LLMs, where each line represents a single LLM. The x-axis shows feature names and the y-axis shows the coefficient values. As this is a static plot, we only plot the top 10 important features, see the Feature Importance Plot section for details. From the figure above, we can see that Pay_1 is the most important feature, with a wide range of coefficient values. The second and the third important variables are PAY_AMT1 and PAY_3, respectively.

In general, this plot can be roughly interpreted in the following way.

• A feature is important when most of its coefficients (absolute values) are large. A feature is shown to have a monotonic increasing effect if all of its coefficients are positive and vice versa.

• When most of the coefficients of a feature are close to zero, it is implied that this feature is trivial and probably can be removed.

• When the range of the coefficients of a feature is large, it is implied that this feature may have a nonlinear effect on the final prediction.

5.9.4.3. LLM Violin Plot

The violin plot corresponds to the keyword “llm_violin”.

exp.model_interpret(model="ReLUDNN", show="llm_violin", figsize=(5, 4))

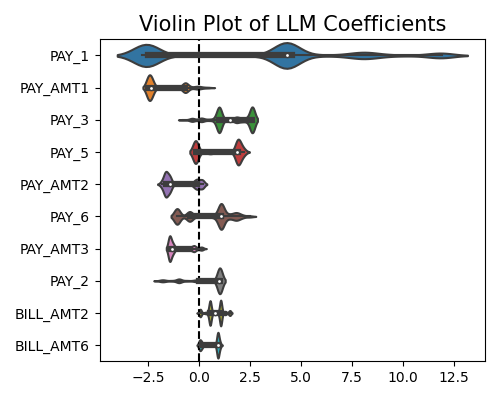
Similar to the parallel coordinate plot, this plot shows the LLM coefficient distribution per feature weighted by the sample size of each LLM.

5.9.4.4. Feature Importance Plot

This global feature importance plot (with the keyword “global_fi”) visualizes the most important features in descending order.

exp.model_interpret(model="ReLUDNN", show="global_fi", figsize=(5, 4))

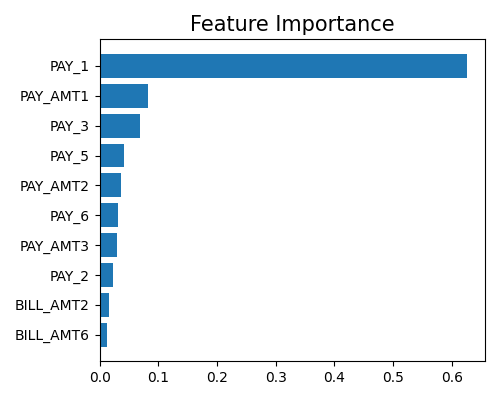
To calculate the feature importance, we first calculate the squared sum of LLM coefficients per feature; then the importance values are normalized such that their sum equals one.

5.9.4.5. LLM profile plot

The local linear profile plot (with the keyword “global_effect_plot”) shows the marginal linear functions upon centering, and it should be used together with the parameter uni_feature.

exp.model_interpret(model="ReLUDNN", show="global_effect_plot", uni_feature="PAY_1", original_scale=True, figsize=(5, 4))

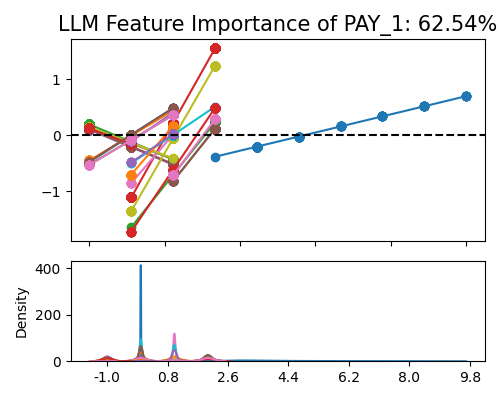
In this plot, each line represents an LLM. The x-axis shows unique values of the specified feature (PAY_1 in this example), and the y-axis is the marginal effect (coefficient times feature values) of that feature. To make this plot more elegant, we only visualize the top 30 LLMs and the marginal effects are all de-meaned.

5.9.4.6. LLM pairwise plot

This plot also uses the keyword “global_effect_plot”, and it will be triggered as two features are specified in bi_features.

exp.model_interpret(model="ReLUDNN", show="global_effect_plot", bi_features=["PAY_1", "PAY_3"], original_scale=True, figsize=(5, 4))

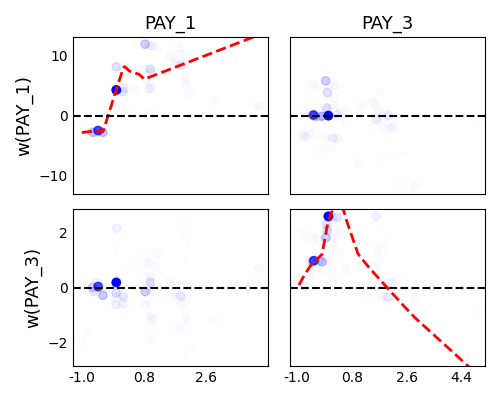
The plot above consists of 2 * 2 subplots, which are used to show how the coefficient would change as the feature value changes. In particular, each point represents an LLM, and the x-axis is calculated as the average of samples belonging to that LLM. The diagonal subplots show the main effect of the selected two features, and the off-diagonal subplots show the interaction effects.

5.9.5. Local Interpretation

5.9.5.1. Local Feature Contribution plot

The local feature importance plot (with the keyword “local_fi”) shows the prediction decomposition of a single training sample.

exp.model_interpret(model="ReLUDNN", show="local_fi", sample_id=0, centered=False, original_scale=True, figsize=(5, 4))

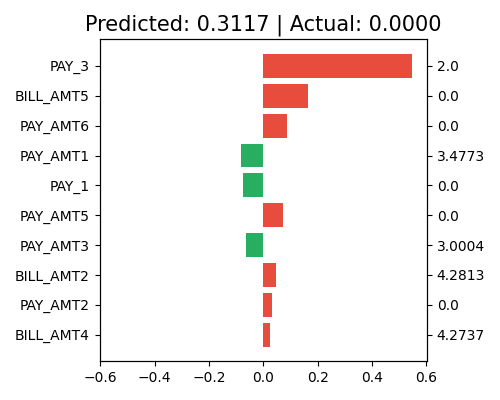
The definition of Weight and Effect can be found in the introduction for GLM. The stems represent the coefficients and the bars show the effect. Similarly, we provide the centered option, as shown below.

exp.model_interpret(model="ReLUDNN", show="local_fi", sample_id=0, centered=True, original_scale=True, figsize=(5, 4))

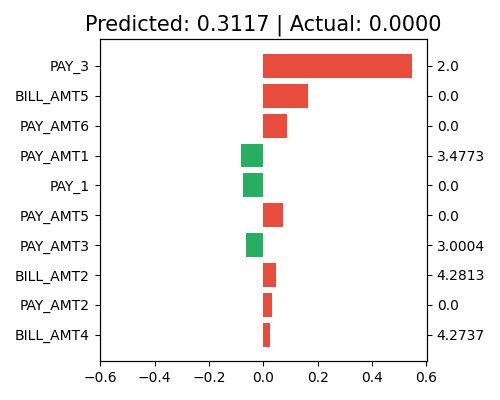
After centering, we find that PAY_3 contributes the most to the final prediction, while PAY_1 is still the most sensitive feature.

5.9.6. Examples

Example 1: Friedman

‘Friedman #1’ regression problem, generated via Scikit-Learn. Inputs X are independent features uniformly distributed on the interval [0, 1]. The output y is created according to the formula:

\[\begin{align} y(x) = 10\ \sin(\pi x_{0} x_{1}) + 20 (x_{2} - 0.5)^{2} + 10 x_{3} + 5 x_{4} + \epsilon. \end{align}\]

Out of the n_features features, only 5 are used to compute y. The remaining features are independent of y.

• ReLU DNN Regression (Friedman)

Examples 2: Taiwan Credit

The second example below demonstrates how to use PiML’s high-code APIs for the TaiwanCredit dataset from the UCI repository. This dataset comprises the credit card details of 30,000 clients in Taiwan from April 2005 to September 2005, and more information can be found on the TaiwanCreditData website. The FlagDefault variable serves as the response for this classification problem.

• ReLU DNN Classification (Taiwan Credit)